Home > Practice > Arithmetic Aptitude > Pipes and Cisterns > Miscellaneous
31. Two pipes A and B can fill a tank in 20 and 30 hours respectively. Both the pipes are opened to fill the tank but when the tank is one - third full, a leak develops in the tank through which one - third water supplied by both the pipes gose out. The total time taken to fill the tank is?
So, A and B together can fill the tank in 12 hrs,
part is filled by (A + B) in
Since the leak empties one - third water, so time taken to fill the tank
= Time taken by (A + B) to fill the whole tank + Time taken by (A + B) to fill one - third tank
= (12 + 4)
= 16 hours
Solution:
Part filled by (A + B) in 1 hourSo, A and B together can fill the tank in 12 hrs,
part is filled by (A + B) in
Since the leak empties one - third water, so time taken to fill the tank
= Time taken by (A + B) to fill the whole tank + Time taken by (A + B) to fill one - third tank
= (12 + 4)
= 16 hours
32. Two pipes can fill a tank in 40 and 48 minutes respectively and a waste pipe can empty 3 gallons per minutes. All the three pipes working together can fill the tank in 30 minutes, The capacity of the tank is-
Solution:
Work done by the waste pipe in 1 minute
33. An outlet pipe can empty a cistern in 3 hours. In what time will empty of the cistern?
Time taken to empty Part of the cistern
Solution:
The outlet pipe empties the one complete cistern in 3 hoursTime taken to empty Part of the cistern
34. A tank is 7 metre long and 4 meter wide wide. At what speed should water run through a pipe 5 cm broad and 4 cm deep so that in 6 hours and 18 minutes water level in the tank rises by 4.5 meter?
∴ Volume of water that flowed in the in 1 minutes
= (5 × 4 × x) = 20 x cu.cm.
∴ Volume of water that flowed in the tank in 6 hours 18 minutes.
i.e. (6 × 60 + 18) = 378 minutes
= 2x × 378 cu. cm.
According to question,
Solution:
Rate of flow of water = x cm/minute∴ Volume of water that flowed in the in 1 minutes
= (5 × 4 × x) = 20 x cu.cm.
∴ Volume of water that flowed in the tank in 6 hours 18 minutes.
i.e. (6 × 60 + 18) = 378 minutes
= 2x × 378 cu. cm.
According to question,
35. Two pipes can fill a tank in 12 hours and 16 hours respectively. A third pipe can empty the tank in 30 hours. If all three pipes are opened and functions simultaneously, how much time will the tank take to be full?( in hours )
Second pipe fill the tank in 1 hour = part of tank
Third pipe empty the tank in 1 hour = part of tank
When all three pipes are opened simultaneously, part of the tank filled in 1 hour
LCM of 12, 16 and 30 = 240
∴ Required time taken by all the three pipes
Solution:
First pipe fill the tank in 1 hour = part of tankSecond pipe fill the tank in 1 hour = part of tank
Third pipe empty the tank in 1 hour = part of tank
When all three pipes are opened simultaneously, part of the tank filled in 1 hour
LCM of 12, 16 and 30 = 240
∴ Required time taken by all the three pipes
36. A tap can completely fill a water tank in 8 hours. The water tank has a hole in it through which the water leaks out. The leakage will cause the full water tank to get empty in 12 hours. How much time will it take for the tap the the tank completely with the hole?
∴ The tank will be filled in 24 hours
Solution:
Net part filled in 1 hour∴ The tank will be filled in 24 hours
37. A tank can be filled by pipe A in 2 hours and pipe B in 6 hours. At 10 A.M. pipe A was opened. At what time will the tank be filled if pipe B is opened at 11 A.M. ?
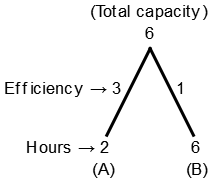
Pipe A will fill 3 units till 11 A.M. Remaining capacity
= 6 - 3
= 3 units
Now both pipes will fill the tank in
So, A.M., tank will be filled = 11.45 A.M.
Solution:

Pipe A will fill 3 units till 11 A.M. Remaining capacity
= 6 - 3
= 3 units
Now both pipes will fill the tank in
So, A.M., tank will be filled = 11.45 A.M.
38. A water tank can be filled by a tap in 30 minutes and another tap can fill it in 60 minutes. If both taps are kept open for 5 minutes and then the first tap is closed, how long will it take foe the tank to be filled ?
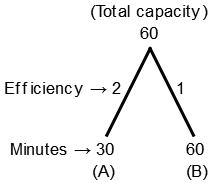
(A + B)'s filling (2 + 1) = 3 units/min
In 5 minutes they will fill 3 × 5 = 15 units
Remaining capacity = 60 - 15 = 45 units
Second pipe (B) fills it in
Solution:

(A + B)'s filling (2 + 1) = 3 units/min
In 5 minutes they will fill 3 × 5 = 15 units
Remaining capacity = 60 - 15 = 45 units
Second pipe (B) fills it in
39. A pipe can fill a tank in x hours and another can empty it in y hours. In how many hours they together fill it in ( y > x) ?
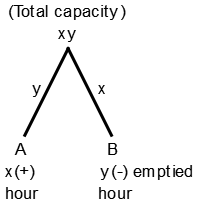
Time will be taken by both of them to fill the tank
Solution:

Time will be taken by both of them to fill the tank
40. A water tap fills a tub in 'p' hours and a sink at the bottom empties it in 'q' hours. If p < q and both tap and sink are opened the tank is filled in 'r' hours, then the relation between p, q, r :
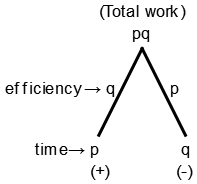
Net efficiency = q - p (∵ q > p)
Time required
Solution:

Net efficiency = q - p (∵ q > p)
Time required