Home > Practice > Arithmetic Aptitude > Alligation or Mixture > Miscellaneous
31. How many litres of water should be added to a 30 litre mixture of milk and water containing milk and water in the ratio of 7 : 3 such that the resultant mixture has 40% water in it?
And quantity of water in the mixture
Let water to be mixed 'a' litre
Then,
Hence, 5 litres water mixed in the mixture.
Solution:
Total quantity of mixtureAnd quantity of water in the mixture
Let water to be mixed 'a' litre
Then,
Hence, 5 litres water mixed in the mixture.
32. Two vessels A and B contain spirit and water mixed in the ratio 5 : 2 and 7 : 6 respectively. Find the ratio in which these mixtures be mixed to obtain a new mixture in vessel C containing spirit and water in the ratio 8 : 5 ?
Spirit in 1 litre mixture in A = litre;
Cost price of 1 litre mixture in A = Rs.
Spirit in 1 litre mixture of B = litre;
Cost price of 1 litre mixture in B = Rs.
Spirit in 1 litre mixture of C = litre;
Mean price = Rs.
By the rule of alligation, we have:
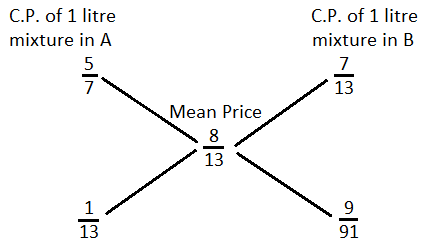
∴ Request ratio = : = 7 : 9
Solution:
Let the Cost price of spirit be Rs. 1 per litreSpirit in 1 litre mixture in A = litre;
Cost price of 1 litre mixture in A = Rs.
Spirit in 1 litre mixture of B = litre;
Cost price of 1 litre mixture in B = Rs.
Spirit in 1 litre mixture of C = litre;
Mean price = Rs.
By the rule of alligation, we have:

∴ Request ratio = : = 7 : 9
33. The respective ratio of milk and water in the mixture is 4 : 3. If 6 litres of water is added to this mixture, the respectively ratio of milk and water becomes 8 : 7. What is the quantity of milk in the original mixture ?
Quantity of water = 3x litres
On adding 6 litres of water, we get
∴ Required quantity of milk
= 4x
= 4 × 12
= 48 litres
Solution:
Let the quantity of milk and water in initial mixture be 4x and 3x litres.Quantity of water = 3x litres
On adding 6 litres of water, we get
∴ Required quantity of milk
= 4x
= 4 × 12
= 48 litres
34. 35 kg of type A sandal powder, which costs Rs. 614 per kg, was mixed with a certain amount of type B sandal powder, which costs Rs. 695 per kg. Then the mixture was sold at the rate of Rs. 767 per kg and 18% profit was earned. What was the amount (in kg) of type B sandal powder in the mixture ?
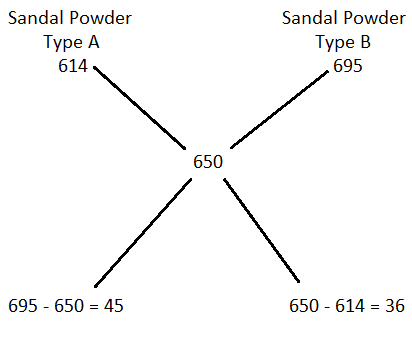
Ratio = 5 : 4
∴ Quantity of A type of sandal is 35 kg
∴ 5x = 35 kg
∴ x = 7 kg
Thus B type sandal = 7 × 4 = 28 kg
Solution:
Cost price of mixture
Ratio = 5 : 4
∴ Quantity of A type of sandal is 35 kg
∴ 5x = 35 kg
∴ x = 7 kg
Thus B type sandal = 7 × 4 = 28 kg
35. Two vessels A and B contain milk and water mixed in the ratio 8 : 5 and 5 : 2 respectively. The ratio in which these two mixtures be mixed to get a new mixture containing milk, is-
Cost price of 1 litre mixture in A = Rs.
Milk in 1 litre mixture in B = litre;
Cost price of 1 litre mixture in B = Rs.
Milk in 1 litre of final mixture
Mean price = Rs.
By the rule of alligation, we have:
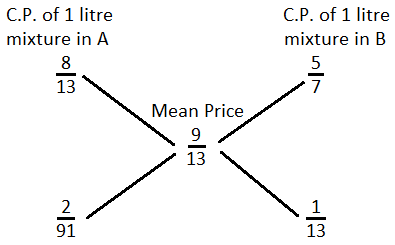
∴ Required ratio = : = 2 : 7
Solution:
Let cost of 1 litre milk be Rs. 1Milk in 1 litre mixture in A = litre;Cost price of 1 litre mixture in A = Rs.
Milk in 1 litre mixture in B = litre;
Cost price of 1 litre mixture in B = Rs.
Milk in 1 litre of final mixture
Mean price = Rs.
By the rule of alligation, we have:

∴ Required ratio = : = 2 : 7
36. 20 litres of a mixture contains milk and water in the ratio 3 : 1. Then the amount of milk to be added to the mixture so as to have milk and water in ratio 4 : 1 is-
Quantity of milk
Quantity of water
Let the quantity of milk added be x litres.
According to the question,
Solution:
In 20 litres of mixtureQuantity of milk
Quantity of water
Let the quantity of milk added be x litres.
According to the question,
37. In what ratio must water be mixed with milk costing Rs. 12 per litre to obtain a mixture worth of Rs. 8 per litre?
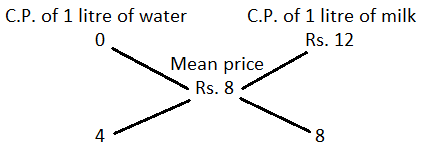
Ratio of water to milk
= 4 : 8
= 1 : 2
Solution:
By the rule of alligation :
Ratio of water to milk
= 4 : 8
= 1 : 2
38. A milkman mixed some water with milk to gain 25% by selling the mixture at the cost price. The ratio of water and milk is respectively -
∴ Mixture sold for Rs. 125
= = litres
∴ Quantity of mixture = litres
∴ Quantity of milk = 1 litre
∴ Quantity of water = - 1 = litre
∴ Required ratio = : 1 = 1 : 4
Solution:
Cost price of 1 litres of milk = Rs. 100∴ Mixture sold for Rs. 125
= = litres
∴ Quantity of mixture = litres
∴ Quantity of milk = 1 litre
∴ Quantity of water = - 1 = litre
∴ Required ratio = : 1 = 1 : 4
39. A vessel contains a mixture of Grape, Pineapple and Banana juices in the respectively ratio of 4 : 6 : 5. 15 litres of this mixture is taken out and 8 litres of grape juice and 2 litres of pineapple juice is added to the vessel. If the resultant quantity of grape juice is 10 litres less than the resultant quantity of pineapple juice, what was the initial quantity of mixture in the vessel ? ( in litres)
Total initial quantity of juice in the vessel
= 4x + 6x + 5x
= 15x litres
In 15 litres of juice,
Grape's juice = 4 litres
Pineapple's juice = 6 litres
Banana's juice = 5 litres
Resultant quantity of grape juice is 10 litres less than the resultant quantity of pineapple juice
∴ Initial quantity of mixture
= 15x
= 15 × 9
= 135 litres
Solution:
Let quantity of grape, pineapple and banana juice in the mixture be 4x, 6x and 5x respectivelyTotal initial quantity of juice in the vessel
= 4x + 6x + 5x
= 15x litres
In 15 litres of juice,
Grape's juice = 4 litres
Pineapple's juice = 6 litres
Banana's juice = 5 litres
Resultant quantity of grape juice is 10 litres less than the resultant quantity of pineapple juice
∴ Initial quantity of mixture
= 15x
= 15 × 9
= 135 litres
40. In what ratio must tea at Rs. 62 per kg be mixed with tea at Rs. 72 per kg so that the mixture must be worth Rs. 64.50 per kg?
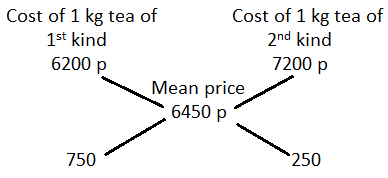
∴ Required ratio
= 750 : 250
= 3 : 1
Solution:
By the rule of alligation :
∴ Required ratio
= 750 : 250
= 3 : 1