Home > Practice > Arithmetic Aptitude > Alligation or Mixture > Miscellaneous
21. In what ratio must a grocer mix two varieties of pulses costing Rs. 15 and Rs. 20 per kg respectively so as to get a mixture worth Rs. 16.50 kg?
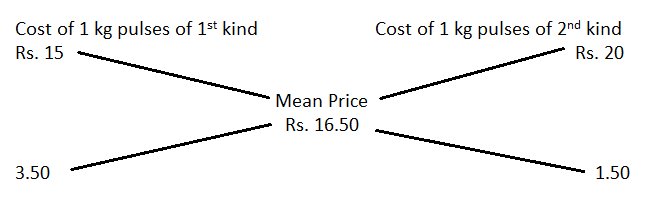
∴ Required rate = 3.50 : 1.50 = 7 : 3
Solution:
By the rule of alligation, we have:
∴ Required rate = 3.50 : 1.50 = 7 : 3
22. A dishonest milkman professes to sell his milk at cost price but he mixes it with water and thereby gains 25%. The percentage of water in the mixture is:
Then, S.P. of 1 litre of mixture = Rs. 1, Gain = 25%
C.P. of 1 litre mixture = Rs. =
By the rule of alligation, we have:
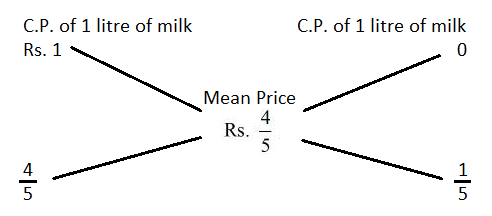
∴ Ratio of milk to water = : = 4 : 1
Hence, percentage of water in the mixture = % = 20%
Solution:
Let C.P. of 1 litre milk be Rs. 1Then, S.P. of 1 litre of mixture = Rs. 1, Gain = 25%
C.P. of 1 litre mixture = Rs. =
By the rule of alligation, we have:

∴ Ratio of milk to water = : = 4 : 1
Hence, percentage of water in the mixture = % = 20%
23. A container contains 40 litres of milk. From this container 4 litres of milk was taken out and replaced by water. This process was repeated further two times. How much milk is now contained by the container?
Solution:
24. A jar full of whisky contains 40% alcohol. A part of this whisky is replaced by another containing 19% alcohol and now the percentage of alcohol was found to be 26%. The quantity of whisky replaced is:
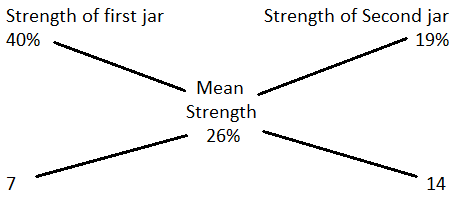
So, ratio of 1st and 2nd quantities = 7 : 14 = 1 : 2
∴ Required quantity replaced =
Solution:
By the rule of alligation, we have:
So, ratio of 1st and 2nd quantities = 7 : 14 = 1 : 2
∴ Required quantity replaced =
25. In what ratio must water be mixed with milk to gain on selling the mixture at cost price?
S.P. of 1 litre of mixture = Rs. 1, Gain = %
∴ C.P. of 1 litre of mixture = =
BY the rule of alligation, we have:
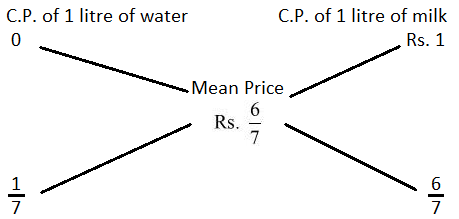
∴ Ration of water and milk = : = 1 : 6
Solution:
Let C.P. of 1 litre milk be Rs. 1S.P. of 1 litre of mixture = Rs. 1, Gain = %
∴ C.P. of 1 litre of mixture = =
BY the rule of alligation, we have:

∴ Ration of water and milk = : = 1 : 6
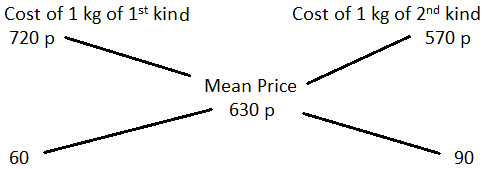
26. Find the ratio in which rice at Rs. 7.20 a kg be mixed with rice at Rs. 5.70 a kg to produce a mixture worth Rs. 6.30 a kg.
∴ Required ratio = 60 : 90 = 2 : 3
Solution:
By the rule of alligation:
∴ Required ratio = 60 : 90 = 2 : 3
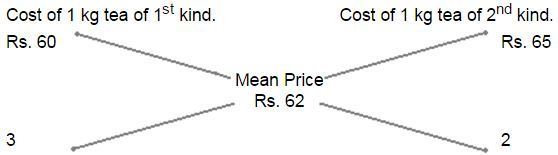
27. In what ratio must a grocer mix two varieties of tea worth Rs. 60 a kg and Rs. 65 a kg so that by selling the mixture at Rs. 68.20 a kg he may gain 10%?
C.P. of 1 kg of the mixture = Rs. = Rs. 62
By the rule of alligation, we have:
∴ Required ratio = 3 : 2
Solution:
S.P. of 1 kg of the mixture = Rs. 68.20, Gain = 10%C.P. of 1 kg of the mixture = Rs. = Rs. 62
By the rule of alligation, we have:

∴ Required ratio = 3 : 2
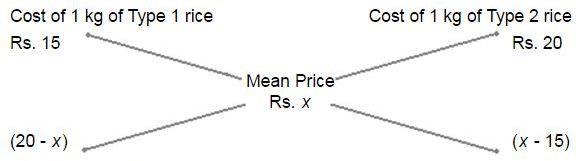
28. The cost of Type 1 rice is Rs. 15 per kg and Type 2 rice is Rs. 20 per kg. If both Type 1 and Type 2 are mixed in the ratio of 2 : 3, then the price per kg of the mixed variety of rice is:
By rule of alligation, we have:
Solution:
Let the price of the mixed variety be Rs. x per kg.By rule of alligation, we have:

29. 8 litres are drawn from a cask full of wine and is then filled with water. This operation is performed three more times. The ratio of the quantity of wine now left in cask to that of water is 16 : 65. How much wine did the cask hold originally?
Then, quantity of wine left in cask after 4 operations
Solution:
Let the quantity of the wine in the cask originally be x litres.Then, quantity of wine left in cask after 4 operations
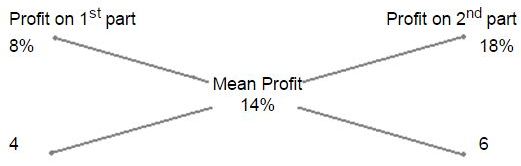
30. A merchant has 1000 kg of sugar, part of which he sells at 8% profit and the rest at 18% profit. He gains 14% on the whole. The quantity sold at 18% profit is:
Ratio of 1st and 2nd parts
= 4 : 6
= 2 : 3
∴ Quantity of 2nd kind
Solution:
By the rule of alligation, we have:
Ratio of 1st and 2nd parts
= 4 : 6
= 2 : 3
∴ Quantity of 2nd kind