Home > Practice > Arithmetic Aptitude > Alligation or Mixture > Miscellaneous
11. Weights of two friends Ram and Shyam are in the ratio 4 : 5. If Ram's weight is increased by 10% and total weight of Ram and Shyam become 82.8 kg, with an increases of 15%. By what percent did the weight of Shyam has to be increased?
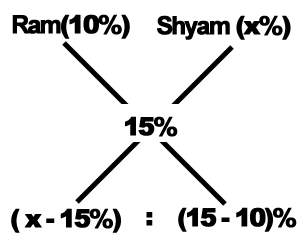
Now, given ratio of Ram and Shayam's weight = 4 : 5
Hence,
Or, x = 19%
Solution:

Now, given ratio of Ram and Shayam's weight = 4 : 5
Hence,
Or, x = 19%
12. A lump of two metals weighing 18 g is worth Rs. 87 but if their weight is interchanged, it would be worth Rs. 78.60. If the price of one metal be Rs. 6.70 per gram, find the weight of the other metal in the mixture.
Cost of (1g of 1st metal + 1g metal of 2nd metal) = Rs. 9.20
Hence cost of 1g of 2nd metal,
= 9.20 - 6.70
= Rs. 2.5
Mean price = Rs.
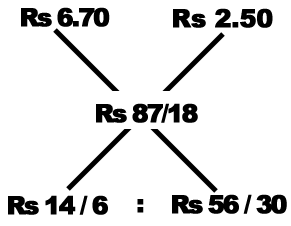
Now,
Quantity of 2nd metal = = 8g
Solution:
Cost of (18g of 1st metal + 18g of 2nd metal) = Rs. 165.60Cost of (1g of 1st metal + 1g metal of 2nd metal) = Rs. 9.20
Hence cost of 1g of 2nd metal,
= 9.20 - 6.70
= Rs. 2.5
Mean price = Rs.

Now,
Quantity of 2nd metal = = 8g
13. A vessel contains milk and water in the ratio 3 : 2. The volume of the contents is increased by 50% by adding water to it. From this resultant solution 30 L is withdrawn and then replaced with water. The resultant ratio of milk water in the final solution is 3 : 7. Find the original volume of the solution.
then, quantity of milk and water,
= and respectively.
After adding water to it, the volume becomes 150%, the quantity of milk and water,
= and
14(3x - 60) = 3(9x + 120)
Or, x = 80 L
Solution:
Let the original volume be x.then, quantity of milk and water,
= and respectively.
After adding water to it, the volume becomes 150%, the quantity of milk and water,
= and
14(3x - 60) = 3(9x + 120)
Or, x = 80 L
14. 3 L water is taken out from vessel full of water and substituted by pure milk. This process is repeated two more times. Finally, the ratio of milk and water in the solution becomes 1728 : 27. Find the volume of the original solution.
n = number of time process of out going repeated.
y = Out going milk in process.
x = Volume of original solution.
F = Final milk left in mixture.
Final quantity of water,
Solution:
We use formula for it wheren = number of time process of out going repeated.
y = Out going milk in process.
x = Volume of original solution.
F = Final milk left in mixture.
Final quantity of water,
15. One quantity of wheat at Rs 9.30 per Kg is mixed with another quality at a certain rate in the ratio 8 : 7. If the mixture so formed be worth Rs 10 per Kg, what is the rate per Kg of the second quality of wheat?
C.P of 1 Kg wheat of 1st kind = 930 p
C.P of 1 Kg wheat of 2nd kind = 100x p
Mean price = 1000 p
By rule of alligation we have required ratio 8 : 7
930 x / (Mean Price) (1000) / (x-10) : 0.7
So we get required ratio, (x-10) : 0.7 :: 8 : 7
⇒ x = 10.80 per Kg
Solution:
Let the rate of second quality be Rs. x per Kg.C.P of 1 Kg wheat of 1st kind = 930 p
C.P of 1 Kg wheat of 2nd kind = 100x p
Mean price = 1000 p
By rule of alligation we have required ratio 8 : 7
930 x / (Mean Price) (1000) / (x-10) : 0.7
So we get required ratio, (x-10) : 0.7 :: 8 : 7
⇒ x = 10.80 per Kg
16. In a zoo, there are Rabbits and Pigeons. If heads are counted, there are 200 and if legs are counted, there are 580. How many pigeons are there?
Legs count = 580
Average Legs count for per head = =

Rabbits : Pigeons = : = 9 : 11
Number of Pigeons = = 110
Solution:
Heads Count = 200Legs count = 580
Average Legs count for per head = =

Rabbits : Pigeons = : = 9 : 11
Number of Pigeons = = 110
17. A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
Let x litres of this liquid be replaced with water.
Quantity of water in new mixture = litres
Quantity of syrup in new mixture = litres
So, part of the mixture replaced
Solution:
Suppose the vessel initially contains 8 litres of liquid.Let x litres of this liquid be replaced with water.
Quantity of water in new mixture = litres
Quantity of syrup in new mixture = litres
So, part of the mixture replaced
18. Tea worth Rs. 126 per kg and Rs. 135 per kg are mixed with a third variety in the ratio 1 : 1 : 2. If the mixture is worth Rs. 153 per kg, the price of the third variety per kg will be:
So, their average price
So, the mixture is formed by mixing two varieties, one at Rs. 130.50 per kg and the other at say, Rs. x per kg in the ratio 2 : 2, i.e., 1 : 1. We have to find x.
By the rule of alligation, we have:

Solution:
Since first and second varieties are mixed in equal proportions.So, their average price
So, the mixture is formed by mixing two varieties, one at Rs. 130.50 per kg and the other at say, Rs. x per kg in the ratio 2 : 2, i.e., 1 : 1. We have to find x.
By the rule of alligation, we have:

19. A can contains a mixture of two liquids A and B is the ratio 7 : 5. When 9 litres of mixture are drawn off and the can is filled with B, the ratio of A and B becomes 7 : 9. How many litres of liquid A was contained by the can initially?
So, the can contained 21 litres of A
Solution:
So, the can contained 21 litres of A
20. A milk vendor has 2 cans of milk. The first contains 25% water and the rest milk. The second contains 50% water. How much milk should he mix from each of the containers so as to get 12 litres of milk such that the ratio of water to milk is 3 : 5?
Milk in 1 litre mixture in 1st can = litre, C.P. of 1 litre mixture in 1st can Rs.
Milk in 1 litre mixture in 2nd can = litre, C.P. of 1 litre mixture in 2nd can Rs.
Milk in 1 litre of final mixture = litre, Mean price = Rs.
By the rule of alligation, we have:
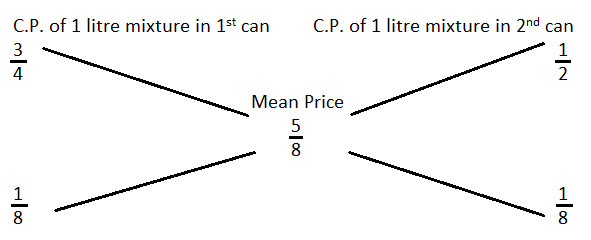
∴ Ratio of two mixtures = : = 1 : 1
So, quantity of mixture taken from each can = = 6 litres
Solution:
Let the cost of 1 litre milk be Rs. 1Milk in 1 litre mixture in 1st can = litre, C.P. of 1 litre mixture in 1st can Rs.
Milk in 1 litre mixture in 2nd can = litre, C.P. of 1 litre mixture in 2nd can Rs.
Milk in 1 litre of final mixture = litre, Mean price = Rs.
By the rule of alligation, we have:

∴ Ratio of two mixtures = : = 1 : 1
So, quantity of mixture taken from each can = = 6 litres