Practice | Hashtable

content Computer Science Arithmetic Aptitude Data Interpretation Logical Reasoning Verbal Reasoning Non-Verbal Reasoning

About About Privacy Policy

Hashtable

Home
Practice
PYQ
Mock Test
Register Free

Home Practice PYQ Mock Test Register Free

Home > Practice > Arithmetic Aptitude > Area > Miscellaneous

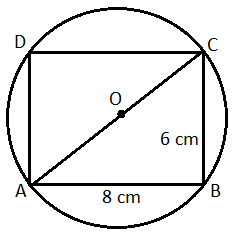
91. The sides of a rectangle are 8 cm and 6 cm. The corners of the rectangle lie on a circle. Find the are a of the circle without the rectangle :

A. 30.6 cm²

B. 39 cm²

C. 42.4 cm²

D. 65.3 cm²

Discuss

Solution:

Diameter of the circle :

\begin{aligned} = A C = \sqrt{{(A B)}^{2} + {(B C)}^{2}} \\ = \sqrt{8^{2} + 6^{2}} \\ = \sqrt{100} c m \\ = 10 c m \end{aligned}

Radius = 5 cm
Required area = (Area of the circle) - (Area of the rectangle)
Area mcq solution image

\begin{aligned} = [(\frac{22}{7} \times 5 \times 5) - (8 \times 6)] c m^{2} \\ = (\frac{550}{7} - 48) c m^{2} \\ = (\frac{214}{7}) c m^{2} \\ = 30.57 c m^{2} \approx 30.6 c m^{2} \end{aligned}

92. A can go round a circular path 8 times in 40 minutes. If the diameter of the circle is increased to 10 times the original diameter, then the time required by A to go round the new path once, travelling at the same speed as before, is :

A. 20 min

B. 25 min

C. 50 min

D. 100 min

Discuss

Solution:

Let original diameter be d metre
Then, its circumference =

(π d)

metres
Time taken to cover

(8 π d)

m = 40 min
New diameter =

(10 d)

m
Then, its circumference =

(π \times 10 d)

m
∴ Time taken to go round it once :

\begin{aligned} = (\frac{40}{8 π d} \times 10 π d) min \\ = 50 min \end{aligned}

93. Area of a rectangle is 150 sq. metre. When the breadth of the same rectangle is increased by 2 metres and the length decreased by 5 metres the area of the rectangle decreases by 30 square metres. What is the perimeter of the square whose sides are equal to the length of the rectangle ?

A. 76 m

B. 72 m

C. 120 m

D. 60 m

Discuss

Solution:

Let the length of rectangle be

l

metre and the breadth of the rectangle be

b

metre
Then area of the rectangle =

l

b

l b

= 150 m² . . . . . (i)
According to the question,

\begin{aligned} (l - 5) \times (b + 2) = 150 - 30 \\ \Rightarrow (l - 5) \times (b + 2) = 120 \\ \Rightarrow l b - 5 b + 2 l - 10 = 120 \\ \Rightarrow 150 - 5 b + 2 l - 10 = 120 \\ \Rightarrow 5 b - 2 l = 20 \\ \Rightarrow \frac{5 \times 150}{l} - 2 l^{2} = 20 l \\ \Rightarrow 2 l^{2} + 20 l - 750 = 0 \\ \Rightarrow l^{2} + 10 l - 375 = 0 \\ \Rightarrow l (l + 25) - 15 (l + 25) = 0 \\ \Rightarrow (l + 15) (l + 25) = 0 \end{aligned}

On solving both equations we get,

l

= 15 m and

b

= 10 m
Side of square = length of rectangle (given)
So, the perimeter of the square :
= 4 ×

l

= 4 × 15
= 60 m

94. If the total surface area of a cube is 864 square cm, find the volume of the cube ?

A. 1728 cm³

B. 1624 cm³

C. 144 cm³

D. 1684 cm³

Discuss

Solution:

Each edges of cube = a cm
∴ Total surface area of cube = 6a²
⇒ 6a² = 864
⇒ a² =

\frac{864}{6}

= 144
⇒ a =

\sqrt{144}

= 12 cm
∴ Volume of cube :
= a³ cm³
= (12 × 12 × 12) cm³
= 1728 cm³

95. A man is walking in a rectangular field whose perimeter is 6 km. If the area of the rectangular field be 2 sq. km, then what is the difference between the length and breadth of the rectangle ?

A. $\frac{1}{2} k m$

B. $1 k m$

C. $1 \frac{1}{2} k m$

D. $2 k m$

Discuss

Solution:

Let the length and breadth of the field be l and b km respectively
Then,
2 (l + b) = 6
⇒ l + b = 3
And lb = 2
(l - b)² = (l + b)² - 4lb
⇒ (l - b)² = 3² - 4 × 2
⇒ (l - b)² = 1
⇒ (l - b) = 1 km

96. If the diagonal and the area of a rectangle are 25 m² and 168 m², what is the length of the rectangle ?

A. 12 m

B. 17 m

C. 24 m

D. 31 m

Discuss

Solution:

Let the length of the rectangle be x metres.
Then, breath of the rectangle =

(\frac{168}{x}) m

\begin{aligned} ∴ \sqrt{x^{2} + {(\frac{168}{x})}^{2}} = 25 \\ \Rightarrow \sqrt{x^{2} + \frac{28224}{x^{2}}} = 25 \\ \Rightarrow x^{2} + \frac{28224}{x^{2}} = 625 \\ \Rightarrow x^{4} - 625 x^{2} + 28224 = 0 \\ \Rightarrow x^{4} - 576 x^{2} - 49 x^{2} + 28224 = 0 \\ \Rightarrow x^{2} (x^{2} - 576) - 49 (x^{2} - 576) = 0 \\ \Rightarrow (x^{2} - 576) (x^{2} - 49) = 0 \\ \Rightarrow x^{2} = 576 o r x^{2} = 49 \\ \Rightarrow x = 24 o r x = 7 \end{aligned}

Hence, length = 24 m and breadth = 7 m

97. A path of uniform width runs round the inside of a rectangular field 38 m long 32 m wide. If the path occupies 600 m², then the width of the path is :

A. 5 m

B. 10 m

C. 18.75 m

D. 30 m

Discuss

Solution:

Let the width of the path be x
Then,

[(38 \times 32) - {(38 - 2 x) (32 - 2 x)}]

= 600

\begin{aligned} \Rightarrow [1216 - (1216 - 140 x + 4 x^{2})] \\ \Rightarrow 4 x^{2} - 140 x + 600 = 0 \\ \Rightarrow x^{2} - 35 x + 150 = 0 \\ \Rightarrow x^{2} - 30 x - 5 x + 150 = 0 \\ \Rightarrow (x - 30) (x - 5) = 0 \\ \Rightarrow x = 5 m [∴ x \neq 30] \end{aligned}

98. The length and breadth of the floor of the room are 20 feet and 10 feet respectively. Square tiles of 2 feet length of different colours are to be laid on the floor. Black tiles are laid in the first row on all sides. If white tiles are laid in the one-third of the remaining and blue tiles in the rest, how many blue tiles will be there ?

A. 16

B. 24

C. 32

D. 48

Discuss

Solution:

Area left after laying black tiles :

\begin{aligned} = [(20 - 4) \times (10 - 4)] sq .ft. \\ = 96 sq .ft. \end{aligned}

Area under white tiles :

\begin{aligned} = (\frac{1}{3} \times 96) sq .ft. \\ = 32 sq .ft. \end{aligned}

Area under blue tiles :

\begin{aligned} = (96 - 32) sq .ft. \\ = 64 sq .ft. \end{aligned}

Number of blue tiles :

\begin{aligned} = \frac{64}{(2 \times 2)} \\ = 16 \end{aligned}

99. Of the two square fields, the area of one is 1 hectare while the other one is broader by 1%. The difference in their areas is :

A. 100 m²

B. 101 m²

C. 200 m²

D. 201 m²

Discuss

Solution:

Area = 1 hect. = 10000 sq. m
Side =

\sqrt{10000}

m = 100 m
Side of the other square = 101 m
Difference in their areas :
= [(101)² - (100)²] m²
= [(101 + 100) (101 - 100)] m²
= 201 m²

1 2 3 4 5 6 7 8 9 10

Sign up for our newsletter

Are you passionate about opportunities in the realm of Computer Science within the government sector? Don't miss out on crucial updates, job openings, and career prospects tailored specifically straight to your inbox.

Email address

By subscribing, you agree with our Terms of Service and Privacy Policy.

Resources

Practice PYQ Mock Test

Company

About us Contact us Privacy policy Terms of service

Hashtable