Home > Practice > Arithmetic Aptitude > Area > Miscellaneous
41. The circumferences of two circle are 132 metres and 176 metres respectively. What is the difference between the area of the larger circle and the smaller circle ?
Solution:
42. The ratio of the radii of two circles is 1 : 3. Then the ratio of their areas is :
Then, required ratio :
Solution:
Let the radii of the two circle be r and 3r respectively.Then, required ratio :
43. The circumference of a circular ground is 88 metres. A strip of land, 3 metres wide, inside and along the circumference of the ground is to be levelled. What is the budgeted expenditure if the levelling costs Rs. 7 per square metre ?
Then,
Area of land strip :
∴ Cost of levelling :
Solution:
Let the radius of the ground be R metres.Then,
Area of land strip :
∴ Cost of levelling :
44. If the circumference of a circle is 100 units, then what will be the length of the arc described by an angle of 20 degrees ?
So, length of the arc :
Solution:
So, length of the arc :
45. If in a triangle, the area is numerically equal to the perimeter, then the radius of the inscribed circle of the triangle is :
Solution:
46. Two equal circle are drawn in square in such a way that a side of the square forms diameter of each circle. If the remaining area of the square is 42 cm2, how much will the diameter of the circle measure ?
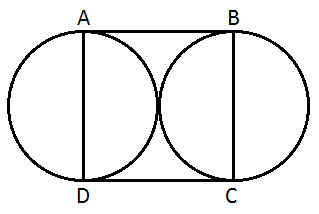
Let length of each side of square = 2π
According to the question,
Solution:

Let length of each side of square = 2π
According to the question,
47. The base of triangle is 15 cm and height is 12 cm the height of another triangle of double the area having base 20 cm is :
Area of first triangle :
According to the question,
Let height of triangle be h cm
Area of new triangle = 180 sq. cm
Base = 20 sq. cm
Solution:
Given base of triangle and its height is 15 cm and 12 cm respectivelyArea of first triangle :
According to the question,
Let height of triangle be h cm
Area of new triangle = 180 sq. cm
Base = 20 sq. cm
48. The difference between the length and breadth of a rectangle is 23 m. If its perimeter is 206 m, then its area is :
(l - b) = 23 and 2(l + b) = 206 or (l + b) = 103
Solving the two equations, we get :
l = 63 and b = 40
∴ Area = (l × b) = (63 × 40)m2 = 2520 m2
Solution:
We have :(l - b) = 23 and 2(l + b) = 206 or (l + b) = 103
Solving the two equations, we get :
l = 63 and b = 40
∴ Area = (l × b) = (63 × 40)m2 = 2520 m2
49. The length of a rectangle is three times of its width. If the length of the diagonal is cm, then the perimeter of the rectangle is :
Then, length = 3x cm
So, length = 24 cm and breadth = 8 cm
∴ Perimeter = [2(24 + 8)] cm = 64 cm
Solution:
Let breadth = x cmThen, length = 3x cm
So, length = 24 cm and breadth = 8 cm
∴ Perimeter = [2(24 + 8)] cm = 64 cm
50. A typist uses a paper 30 cm by 15 cm. He leaves a margin of 2.5 cm at the top and bottom and 1.25 cm on either side. What percentage of paper area is approximately available for typing ?
Area used for typing
= [(30 - 5) × (15 - 2.5)] cm2
= 312.5 cm2
∴ Required percentage :
Solution:
Area of the sheet = (30 × 15) cm2 = 450 cm2 Area used for typing
= [(30 - 5) × (15 - 2.5)] cm2
= 312.5 cm2
∴ Required percentage :