Practice | Hashtable

content Computer Science Arithmetic Aptitude Data Interpretation Logical Reasoning Verbal Reasoning Non-Verbal Reasoning

About About Privacy Policy

Hashtable

Home
Practice
PYQ
Mock Test
Register Free

Home Practice PYQ Mock Test Register Free

Home > Practice > Arithmetic Aptitude > Area > Miscellaneous

81. The breadth of a rectangular field is $\frac{3}{4}$ of its length and its area is 300 sq. metres. What will be the area (in sq. metres) of the garden of breath 1.5 metres developed around the field ?

A. 96 m²

B. 105 m²

C. 114 m²

D. Cannot be determined

Discuss

Solution:

Let the length of the field be x metres
Then, breadth of the field =

\frac{3 x}{4}

metres

\begin{aligned} x \times \frac{3 x}{4} = 300 \\ \Rightarrow x^{2} = 300 \times \frac{4}{3} \\ \Rightarrow x^{2} = 400 \\ \Rightarrow x = 20 \end{aligned}

So, length = 20 m, breadth = 15 m
∴ Area of the garden :

\begin{aligned} = [{(20 + 3) \times (15 + 3)} - (20 \times 15)] m^{2} \\ = [(23 \times 18) - (20 \times 15)] m^{2} \\ = (414 - 300) m^{2} \\ = 114 m^{2} \end{aligned}

82. How many squares with side $\frac{1}{2}$ inch long are needed to cover a rectangle that is 4 feet long and 6 feet wide ?

A. 24

B. 96

C. 3456

D. 13824

Discuss

Solution:

length of rectangle = 4ft = (4 ×12) inch = 48 inch
length of rectangle = 6ft = (6 ×12) inch = 72 inch
∴ Number of squares :

\begin{aligned} = \frac{48 \times 72}{\frac{1}{2} \times \frac{1}{2}} \\ = 13824 \end{aligned}

83. If a square of area $\frac{A}{2}$ is cut off from a given square of area A, then the ratio of diagonal of the cut off square to that of the given square is :

A. 1 : 5

B. 1 : $2 \sqrt{5}$

C. 1 : $\sqrt{5}$

D. 1 : $\sqrt{2}$

Discuss

Solution:

Let the length of diagonal of the bigger square be x and that of the smaller square be y.
Then,

A = \frac{1}{2} x^{2} o r x = \sqrt{2 A}

And,

\frac{A}{2} = \frac{1}{2} y^{2} o r y = \sqrt{A}

\begin{aligned} ∴ Required ratio : \\ = \frac{y}{x} = \frac{\sqrt{A}}{\sqrt{2 A}} = 1 : \sqrt{2} \end{aligned}

84. The length of a room is double its breadth. The cost of colouring the ceiling at Rs. 25 per sq. meter is Rs. 5000 and the cost of painting the four walls at Rs. 240 per sq. metre is Rs. 64800. Find the height of the room :

A. 3.5 m

B. 4 m

C. 4.5 m

D. 5 m

Discuss

Solution:

Let the breadth and height of the room be b metres and h metres respectively.
Then, length of the room = (2b) metres
Area of the ceiling :

\begin{aligned} = (2 b \times b) m \\ = (2 b^{2}) m^{2} \end{aligned}

\begin{aligned} 2 b^{2} = \frac{5000}{25} \\ 2 b^{2} = 200 \\ b^{2} = 100 \\ b = 10 \end{aligned}

So, length = 20 m, breadth = 10 m
Area of 4 walls :

\begin{aligned} = [2 (20 + 10) \times h] m^{2} \\ = (60 h) m^{2} \end{aligned}

\begin{aligned} ∴ 60 h = \frac{64800}{240} \\ \Rightarrow 60 h = 270 \\ \Rightarrow h = \frac{270}{60} \\ \Rightarrow h = 4.5 m \end{aligned}

85. The sides of a triangle are in ratio of $\frac{1}{2} : \frac{1}{3} : \frac{1}{4}$ . If the perimeter is 52 cm, then the length of the smallest side is :

A. 9 cm

B. 10 cm

C. 11 cm

D. 12 cm

Discuss

Solution:

Ratio of sides =

\frac{1}{2} : \frac{1}{3} : \frac{1}{4}

= 6 : 4 : 3
Perimeter = 52 cm
So, sides are :

\begin{aligned} (52 \times \frac{6}{13}) c m \\ (52 \times \frac{4}{13}) c m & \\ (52 \times \frac{3}{13}) c m \end{aligned}

So, a = 24 cm, b = 16 cm, and c = 12 cm
∴ Length of smallest side = 12 cm

86. If x is the length of a median of an equilateral triangle, then its area is :

A. x²

B. $\frac{1}{2} x^{2}$

C. $\frac{\sqrt{3}}{2} x^{2}$

D. $\frac{\sqrt{3}}{3} x^{2}$

Discuss

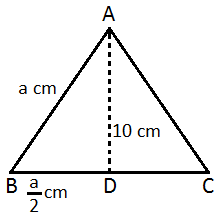
Solution:

Let the side of the triangle be a
Then,

\begin{aligned} a^{2} = {(\frac{a}{2})}^{2} + x^{2} \\ \Leftrightarrow \frac{3 a^{2}}{4} = x^{2} \\ \Leftrightarrow a^{2} = \frac{4 x^{2}}{3} \end{aligned}

∴ Area :

\begin{aligned} = \frac{\sqrt{3}}{4} a^{2} \\ = \frac{\sqrt{3}}{4} \times \frac{4 x^{2}}{3} \\ = \frac{x^{2}}{\sqrt{3}} \\ = \frac{\sqrt{3} x^{2}}{3} \end{aligned}

87. If a square and a rhombus stand on the same base, then the ratio of the areas of the square and the rhombus is :

A. Greater than 1

B. Equal to 1

C. Equal to $\frac{1}{2}$

D. Equal to $\frac{1}{4}$

Discuss

Solution:

A square and a rhombus on the same base are equal in area.

88. Two small circular parks of diameters 16 m and 12 m are to be replaced by a Bigger circular park. What would be the radius of this new park. If the new park has to occupy the same space as the two small parks ?

A. 10 m

B. 15 m

C. 20 m

D. 25 m

Discuss

Solution:

Let the radius of the new park be R m
Then,

\begin{aligned} π R^{2} = π \times 8^{2} + π \times 6^{2} \\ \Rightarrow π R^{2} = 100 π \\ \Rightarrow R^{2} = 100 \\ \Rightarrow R = 10 \end{aligned}

89. If the wheel of the engine of a train $4 \frac{2}{7}$ metres in circumference makes 7 revolutions in 4 seconds, then the speed (in km/hr) of the train is :

A. 27

B. 28

C. 29

D. 30

Discuss

Solution:

Distance covered in 4 sec :

\begin{aligned} = (\frac{30}{7} \times 7) m \\ = 30 m \end{aligned}

Distance covered in 1 sec =

\frac{30}{4}

Distance covered in 1 revolution :

\begin{aligned} = (\frac{30}{4}) m \\ = \frac{15}{2} m \end{aligned}

∴ Required speed :

\begin{aligned} = (\frac{15}{2}) m / s \\ = (\frac{15}{2} \times \frac{18}{5}) k m / h r \\ = 27 k m / h r \end{aligned}

90. A circular swimming pool is surrounded by a concrete wall 4 ft. wide. If the area of the concrete wall surrounding the pool is $\frac{11}{25}$ that of the pool, then the radius of the pool is :

A. 8 ft

B. 16 ft

C. 20 ft

D. 30 ft

Discuss

Solution:

Let the radius of the pool be R ft.
Radius of the pool including the wall = (R + 4)ft.
Area of the concrete wall :

\begin{aligned} = π [{(R + 4)}^{2} - R^{2}] s q . f t \\ = π [(R + 4 + R) (R + 4 - R)] s q . f t \\ = 8 π (R + 2) s q . f t \\ 8 π (R + 2) = \frac{11}{25} π R^{2} \\ \Rightarrow 11 R^{2} = 200 (R + 2) \\ \Rightarrow 11 R^{2} - 200 R - 400 = 0 \\ \Rightarrow 11 R^{2} - 220 R + 20 R - 400 = 0 \\ \Rightarrow 11 R (R - 20) + 20 (R - 20) = 0 \\ \Rightarrow (R - 20) (11 R + 20) = 0 \\ \Rightarrow R = 20 \end{aligned}

∴ Radius of the pool = 20 ft.

1 2 3 4 5 6 7 8 9 10

Sign up for our newsletter

Are you passionate about opportunities in the realm of Computer Science within the government sector? Don't miss out on crucial updates, job openings, and career prospects tailored specifically straight to your inbox.

Email address

By subscribing, you agree with our Terms of Service and Privacy Policy.

Resources

Practice PYQ Mock Test

Company

About us Contact us Privacy policy Terms of service

Hashtable