Practice | Hashtable

content Computer Science Arithmetic Aptitude Data Interpretation Logical Reasoning Verbal Reasoning Non-Verbal Reasoning

About About Privacy Policy

Hashtable

Home
Practice
PYQ
Mock Test
Register Free

Home Practice PYQ Mock Test Register Free

Home > Practice > Arithmetic Aptitude > Area > Miscellaneous

11. The difference between the length and breadth of a rectangle is 23 m. If its perimeter is 206 m, then its area is:

A. 1520 m²

B. 2420 m²

C. 2480 m²

D. 2520 m²

Discuss

Solution:

We have: (l - b) = 23 and 2(l + b) = 206 or (l + b) = 103
Solving the two equations, we get:
l = 63 and b = 40
∴ Area = (l x b) = (63 x 40) m² = 2520 m²

12. The length of a rectangle is halved, while its breadth is tripled. What is the percentage change in area?

A. 25% increase

B. 50% increase

C. 50% decrease

D. 75% decrease

Discuss

Solution:

\begin{aligned} Let original length = x and \\ Original breadth = y \\ Original area = x y \\ New length = \frac{x}{2} \\ New breadth = 3 y \\ New area = (\frac{x}{2} \times 3 y) = \frac{3}{2} x y \\ ∴ Increase % = \frac{1}{2} x y \times \frac{1}{x y} \times 100 \\ = 50 % \end{aligned}

13. The length of a rectangular plot is 20 metres more than its breadth. If the cost of fencing the plot @ 26.50 per metre is Rs. 5300, what is the length of the plot in metres?

A. 40m

B. 50m

C. 120m

D. Data inadequate

Discuss

Solution:

\begin{aligned} Let breadth = x metres \\ Then, length = (x + 20) metres \\ Perimeter = \frac{5300}{26.50} m = 200 m \\ ∴ 2 [(x + 20) + x] = 200 \\ \Rightarrow 2 x + 20 = 100 \\ \Rightarrow 2 x = 80 \\ \Rightarrow x = 40 \\ Hence, length = x + 20 = 60 m \end{aligned}

14. A rectangular field is to be fenced on three sides leaving a side of 20 feet uncovered. If the area of the field is 680 sq. feet, how many feet of fencing will be required?

A. 34

B. 40

C. 68

D. 88

Discuss

Solution:

We have: l = 20 ft and lb = 680 sq. ft.
So, b = 34 ft.
∴ Length of fencing = (l + 2b) = (20 + 68) ft = 88 ft.

15. A tank is 25 m long, 12 m wide and 6 m deep. The cost of plastering its walls and bottom at 75 paise per sq. m, is:

A. Rs. 456

B. Rs. 458

C. Rs. 558

D. Rs. 568

Discuss

Solution:

\begin{aligned} Area to be plastered \\ = [2 (l + b) \times h] + (l \times b) \\ = {[2 (25 + 12) \times 6] + (25 \times 12)} m^{2} \\ = (444 + 300) m^{2} \\ = 744 m^{2} \\ ∴ Cost of Plastering \\ = R s . (744 \times \frac{75}{100}) \\ = R s . 558 \end{aligned}

16. The length of a room is 5.5 m and width is 3.75 m. Find the cost of paving the floor by slabs at the rate of Rs. 800 per square metre.

A. Rs. 15000

B. Rs. 15500

C. Rs. 15600

D. Rs. 16500

Discuss

Solution:

Area of the floor
= (5.5 × 3.75)m²
= 20.625m²
∴ Cost of paying
= Rs. (800 × 20.625)
= Rs. 16500

17. An artist has completed one-fourth of a rectangular oil painting. When he paint another 100 square centimetres of the painting, he would complete three-quarters of the painting. If the height of the oil painting is 10 cm, determine the length (in cm) of the oil panting.

A. 10 cm

B. 15 cm

C. 20 cm

D. 25 cm

Discuss

Solution:

Let the area of the whole painting be x cm²
Then,

\begin{aligned} \Rightarrow \frac{1}{4} x + 100 = \frac{3}{4} x \\ \Rightarrow \frac{1}{2} x = 100 \\ \Rightarrow x = 200 \end{aligned}

∴ Area of painting = 200 cm²
And, Height = 10 cm
Length of painting :

\begin{aligned} = (\frac{200}{10}) c m \\ = 20 c m \end{aligned}

18. The length of a rectangle is increased by 60%. By what percent would the width have to be decreased so as to maintain the same area ?

A. $37 \frac{1}{2} %$

B. $60 %$

C. $75 %$

D. $120 %$

Discuss

Solution:

Let original length = x and original breadth = y
Then, original area = xy
New length :

\begin{aligned} = \frac{160 x}{100} \\ = \frac{8 x}{5} \end{aligned}

Let the new breadth = z
Then,

\begin{aligned} \Rightarrow \frac{8 x}{5} \times z = x y \\ \Rightarrow z = \frac{5 y}{8} \end{aligned}

∴ Decrease in breadth :

\begin{aligned} = (\frac{3 y}{8} \times \frac{1}{y} \times 100) % \\ = 37 \frac{1}{2} % \end{aligned}

19. The following squares represent the monthly income of two families

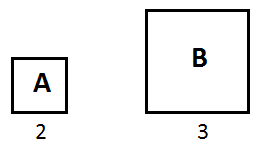
If the monthly income of family A is Rs. 40000, the monthly income of family B is ?

A. Rs. 50000

B. Rs. 60000

C. Rs. 90000

D. Rs. 120000

Discuss

Solution:

\frac{Monthly income of family A}{Monthly income of family B}

= \frac{Area of square A}{Area of square B}

\begin{aligned} \Rightarrow \frac{40000}{x} = \frac{2^{2}}{3^{2}} \\ \Rightarrow x = (\frac{40000 \times 9}{4}) \\ \Rightarrow x = 90000 \end{aligned}

20. What will be the length of the diagonal of that square plot whose area is equal to the area of a rectangular plot of length 45 metres and breadth 40 metres ?

A. 45.5 metres

B. 60 metres

C. 75 metres

D. Data inadequate

Discuss

Solution:

\begin{aligned} Area : \\ = (45 \times 40) m^{2} \Leftrightarrow \frac{1}{2} \times {(Diagonal)}^{2} \\ = 1800 \Leftrightarrow Diagonal \\ = 60 m \end{aligned}

1 2 3 4 5 6 7 8 9 10

Sign up for our newsletter

Are you passionate about opportunities in the realm of Computer Science within the government sector? Don't miss out on crucial updates, job openings, and career prospects tailored specifically straight to your inbox.

Email address

By subscribing, you agree with our Terms of Service and Privacy Policy.

Resources

Practice PYQ Mock Test

Company

About us Contact us Privacy policy Terms of service

Hashtable