Home > Practice > Arithmetic Aptitude > Area > Miscellaneous
61. The area of the largest triangle that can be inscribed in a semi-circle of radius r, is :
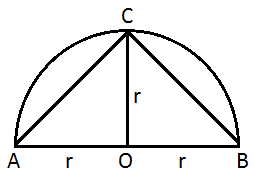
Solution:
Required area :
62. If radius of a circle is 3 cm, what is the area of the circle in sq. cm ?
Area of circle :
Solution:
Given: Radius of a circle = 3 cmArea of circle :
63. The base of an isosceles is 14 cm and its perimeter is 36 cm. Find its area.
Perimeter of an isosceles triangle = 36 cm
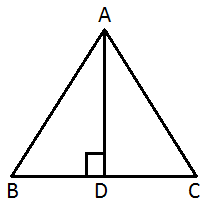
BD = DC = 7cm
From ΔABD
By using Pythagoras theorem :
∴ Area of ΔABC
Solution:
Let each equal side of isosceles triangle be x cmPerimeter of an isosceles triangle = 36 cm

BD = DC = 7cm
From ΔABD
By using Pythagoras theorem :
∴ Area of ΔABC
64. The total cost of flooring a room at Rs. 8.50 per square metre is Rs. 510. If the length of the room is 8 m, its breadth is :
∴ Breadth of the room :
Solution:
Area of the floor :∴ Breadth of the room :
65. The diagonal of a rectangular field is 15 metres and the difference between its length its length and width is 3 metres. The area of the rectangular field is :
Then,
And,
Hence, area of the field
Solution:
Let l and b be the length and breadth of the rectangle respectively.Then,
And,
Hence, area of the field
66. A room 5m × 8 m is to be carpeted leaving a margin of 10 cm from each wall. If the cost of the carpet is Rs. 18 per sq. meter, the cost of carpeting the room will be :
= [(5 - 0.20) × (8 - 0.20)] m2
= (4.8 × 7.8) m2
= 37.44 m2
∴ Cost of carpeting :
= Rs. (37.44 × 18)
= Rs. 673.92
Solution:
Area of the carpet := [(5 - 0.20) × (8 - 0.20)] m2
= (4.8 × 7.8) m2
= 37.44 m2
∴ Cost of carpeting :
= Rs. (37.44 × 18)
= Rs. 673.92
67. The length of a rectangular plot is thrice its breadth. If the area of the rectangular plot is 7803 sq. mtr, what is the breadth of the rectangular plot ?
Then, length of the plot = (3x) metres
x × 3x = 7803
⇒ 3x2 = 7803
⇒ x2 = 2601
⇒ x =
⇒ x = 51 m
Solution:
Let the breadth of the plot be x metres Then, length of the plot = (3x) metres
x × 3x = 7803
⇒ 3x2 = 7803
⇒ x2 = 2601
⇒ x =
⇒ x = 51 m
68. A coaching institute wants to execute tiling work for one of its teaching halls 60 m long and 40 m wide with a square tile of 0.4 m side. If each tile costs Rs. 5, the total cost of tiles would be :
∴ Total cost of tiles :
= Rs. (15000 × 5)
= Rs. 75000
Solution:
Number of tiles required :∴ Total cost of tiles :
= Rs. (15000 × 5)
= Rs. 75000
69. The ratio of the area of a square to that of the square drawn on diagonal is :
Solution:
70. The area of the four walls of a room is 120 m2 and the length is twice the breadth. If the height of the room is 4 m, then the area of the floor is :
Area of 4 walls = [2(2x + x)× 4] m2 = (24x) m2
∴ 24x = 120
⇒ x = 5
So, length = 10 m, and breadth = 5 m
Area of the floor = (10 × 5) m2 = 50 m2
Solution:
Let the breadth = x metres and length = (2x) metresArea of 4 walls = [2(2x + x)× 4] m2 = (24x) m2
∴ 24x = 120
⇒ x = 5
So, length = 10 m, and breadth = 5 m
Area of the floor = (10 × 5) m2 = 50 m2