Home > Practice > Arithmetic Aptitude > Area > Miscellaneous
51. The adjoining figure contains three squares with areas of 100, 16 and 49 lying side by side as shown. By how much should the area of the middle square be reduced in order that the total length PQ of the resulting three squares is 19 ?
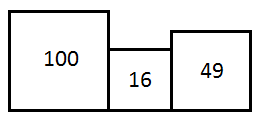
Side of middle square = = 4
Reduction in PQ = (21 - 19) = 2
New side of middle square = (4 - 2) = 2
∴ Reduction in area of middle square = (42 - 22) = 12

Solution:
PQ = + + = (10 + 4 + 7) = 21Side of middle square = = 4
Reduction in PQ = (21 - 19) = 2
New side of middle square = (4 - 2) = 2
∴ Reduction in area of middle square = (42 - 22) = 12
52. The three sides of a triangular field are 20 metres, 21 metres and 29 metres long respectively. The area of the field is :
So, it is a right-angled triangle with base = 20 m and height = 21 m
∴ Area = m2 = 210 m2
Solution:
Since (20)2 + (21)2 = (29)2 So, it is a right-angled triangle with base = 20 m and height = 21 m
∴ Area = m2 = 210 m2
53. The diagonal of a square is cm. The diagonal of another square whose area is double that of the first square, is :
Area of new square = (2 × 16) cm2 = 32 cm2
Solution:
Area of new square = (2 × 16) cm2 = 32 cm2
54. What will be the area of 4 metres high wall on all four sides of a rectangular hall having perimeter 64 m ?
⇒ 2(l + b) = 64
∴ Area of 4 walls
= 2(l + b) × h
= (64 × 4) m2
= 256 m2
Solution:
Perimeter = 64 m ⇒ 2(l + b) = 64
∴ Area of 4 walls
= 2(l + b) × h
= (64 × 4) m2
= 256 m2
55. The altitude of an equilateral triangle of side cm is :
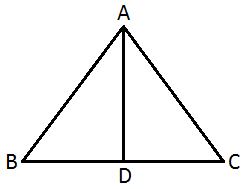
In an equilateral triangle, the altitude and the median coincide.
So, BC = DC = cm = cm
Let the length of the altitude AD be x cm
Then, in right angled ΔADB,
AB2 = AD2 + BD2
⇒ = x2 +
⇒ x2 = (12 - 3)
⇒ x2 = 9
⇒ x = 3 cm
Solution:
Let ABC be the equilateral triangle and AD be the altitude on base BC
In an equilateral triangle, the altitude and the median coincide.
So, BC = DC = cm = cm
Let the length of the altitude AD be x cm
Then, in right angled ΔADB,
AB2 = AD2 + BD2
⇒ = x2 +
⇒ x2 = (12 - 3)
⇒ x2 = 9
⇒ x = 3 cm
56. One of the diagonals of a rhombus is double the other diagonal. Its area is 25 sq. cm. The sum of the diagonal is ?
∴ Sum of lengths of diagonals = (5 + 10) cm = 15 cm
Solution:
∴ Sum of lengths of diagonals = (5 + 10) cm = 15 cm
57. Cost of fencing a circular plot at the rate of Rs. 15 per metre is Rs. 3300. What will be the cost of flooring the plot at the rate of Rs. 100 per square metre ?
Area of the plot :
∴ Cost of flooring :
Solution:
Circumference of the plot :Area of the plot :
∴ Cost of flooring :
58. The ratio of the circumferences of two circles is 2 : 3. What is the ratio of their areas ?
Solution:
59. A circular road runs around a circular garden. If the difference between the circumference of the outer circle and the inner circle is 44 m, the width of the road is :
Then,
Solution:
Let the radii of the outer and inner circle be R and r respectivelyThen,
60. The area of the greatest circle which can be inscribed in a square whose perimeter is 120 cm, is :
Radius of the required circle :
Solution:
Side of the square :Radius of the required circle :