Home > Practice > Arithmetic Aptitude > Area > Miscellaneous
71. The perimeter of an isosceles triangle is equal to 14 cm and the lateral side is to the base in the ratio 5 : 4. The area of the triangle is :
Then,
5x + 5x = 4x + 14
⇒ 14 x = 14
⇒ x = 1
So, a = 5 cm, b = 5 cm, c = 4 cm
(s - a) = 2 cm, (s - b) = 2 cm, (s - c) = 3 cm
∴ Area of the triangle :
Solution:
Let the sides of the triangle be 5x, 5x and 4x cm respectivelyThen,
5x + 5x = 4x + 14
⇒ 14 x = 14
⇒ x = 1
So, a = 5 cm, b = 5 cm, c = 4 cm
(s - a) = 2 cm, (s - b) = 2 cm, (s - c) = 3 cm
∴ Area of the triangle :
72. The areas of two equilateral triangles are in the ratio 25 : 36. Their altitudes will be in the ratio :
Then,
And
Solution:
Let the length of sides of the two triangles be a1 and a2 respectively and their altitudes be h1 and h2 respectively.Then,
And
73. A diagonal of a rhombus is 6 cm. If its area is 24 cm2 then the length of each side of the rhombus is :
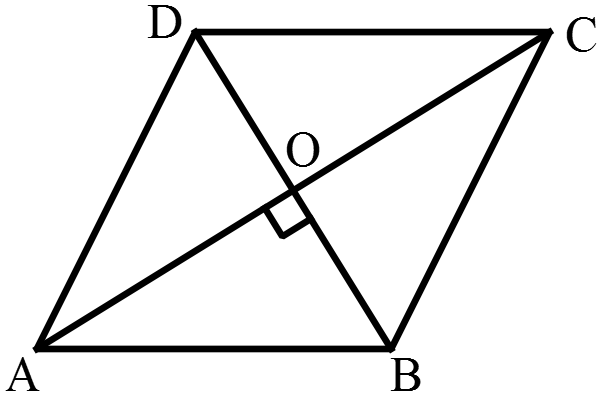
Solution:

74. The magnitude of the area of a circle is seven times that of its circumference. What is the circumference (in units) of the circle ?
Solution:
75. A small disc of radius r is cut out from a disc of radius R. The weight of the disc which now has a hole in it, is reduced to of the original weight. If R = xr, what is the value of x ?
Solution:
Since weight of the disc is proportional to its area, we have :
76. The area of the largest circle, that can be drawn inside a rectangle with side 18 cm by 14 cm, is :
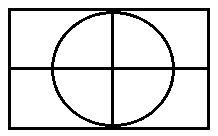
Radius of the required circle :
Area of the circle :
Solution:

Radius of the required circle :
Area of the circle :
77. If the radius of a circle is increased by 75%, then its circumference will increase by :
Then, original circumference = cm
New radius :
New circumference :
Increase in circumference :
Increase % :
Solution:
Let original radius be R cmThen, original circumference = cm
New radius :
New circumference :
Increase in circumference :
Increase % :
78. A plate on square base made of brass is of length x cm and width 1 mm. The plate weights 4725 gm. If 1 cubic cm cm of brass weight 8.4 grams, then the value of x is :
Volume of the plate of square base = Area of base × height
According to the question,
Solution:
Given length and width of a square base plate of brass is x cm and 1 mmVolume of the plate of square base = Area of base × height
According to the question,
79. What would be the area of a rectangle whose area is equal to the area of a circle of radius 7 cm ?
Given area of rectangle :
= Area of circle
=
= 154 cm2
Solution:
Radius of circle = 7cmGiven area of rectangle :
= Area of circle
=
= 154 cm2
80. The perimeter of a rectangle is 60 metres. If its length is twice its breadth, then its area is :
Then, length of the rectangle = 2x metres
⇒ 2(2x + x) = 60
⇒ 6x = 60
⇒ x = 10
So, length = 20 m, breadth = 10 m
∴ Area = (20 × 10) m2 = 200 m2
Solution:
Let the breadth of the rectangle be x metresThen, length of the rectangle = 2x metres
⇒ 2(2x + x) = 60
⇒ 6x = 60
⇒ x = 10
So, length = 20 m, breadth = 10 m
∴ Area = (20 × 10) m2 = 200 m2