Practice | Hashtable

content Computer Science Arithmetic Aptitude Data Interpretation Logical Reasoning Verbal Reasoning Non-Verbal Reasoning

About About Privacy Policy

Hashtable

Home
Practice
PYQ
Mock Test
Register Free

Home Practice PYQ Mock Test Register Free

Home > Practice > Arithmetic Aptitude > Area > Miscellaneous

31. The diameter of a circle is equal to the perimeter of a square whose area is 3136 cm² . What is the circumference of the circle ?

A. 352 cm

B. 704 cm

C. 39424 cm

D. 1024 cm

Discuss

Solution:

Area of square = 3136 cm²
Side of squared =

\sqrt{3136}

= 56 cm
Perimeter of square :
= 4a
= (4 × 56) cm
= 224 cm
= diameter of circle
∴ Circumference of circle :

\begin{aligned} = π d \\ = \frac{22}{7} \times 224 \\ = 704 cm \end{aligned}

32. The area of a rectangular field is 2100 sq. meters. If the field is 60 metres long, what is its perimeter ?

A. 180 m

B. 210 m

C. 240 m

D. Cannot be determined

Discuss

Solution:

\begin{aligned} Breadth = \frac{Area}{Length} \\ = (\frac{2100}{60}) m \\ = 35 m \\ ∴ Perimeter = 2 (60 + 35) m \\ = 190 m \end{aligned}

33. How many metres of carpet 63 cm wide will be required to cover the floor of a room 14 metres by 9 metres ?

A. 185 metres

B. 200 metres

C. 210 metres

D. 220 metres

Discuss

Solution:

Area of the floor = (14 × 9) m² = 126 m²
∴ Length of the carpet :

\begin{aligned} = (\frac{126}{63} \times 100) m \\ = 200 metres \end{aligned}

34. If the length and breadth of a rectangular field are increased, the area increases by 50%. If the increase in length was 20 %, by what percentage was the breadth increased ?

A. 20%

B. 25%

C. 30%

D. Data inadequate

Discuss

Solution:

Let the original length and breadth of the rectangle be l and b respectively
Then, original area = lb
New length = 120% of l =

\frac{6 l}{5}

New area = 150% of lb =

\frac{3 l b}{2}

New breadth :

\begin{aligned} = (\frac{3 l b}{2} \times \frac{5}{6 l}) \\ = \frac{5 b}{4} \end{aligned}

Increase in breadth :

\begin{aligned} = (\frac{5 b}{4} - b) \\ = \frac{b}{4} \end{aligned}

∴ Increase % :

\begin{aligned} = (\frac{b}{4} \times \frac{1}{b} \times 100) % \\ = 25 % \end{aligned}

35. Total area of 64 small squares of a chessboard is 400 sq. cm. There is 3 cm wide border around the chess board. What is the length of the side of the chess board ?

A. 17 cm

B. 20 cm

C. 23 cm

D. 26 cm

Discuss

Solution:

Area of each square :

\begin{aligned} = (\frac{400}{64}) c m^{2} \\ = 6.25 c m^{2} \end{aligned}

Side of each small square :

\begin{aligned} = \sqrt{6.25} c m \\ = 2.5 c m \end{aligned}

Since there are 8 squares along each side of the chess board, we have :
Side = [(8 × 2.5) + 6] cm
= 26 cm

36. Area of a square natural lake is 50 sq. kms. A driver wishing to cross the lake diagonally, will have to swim a distance of :

A. 10 miles

B. 12 miles

C. 15 miles

D. None of these

Discuss

Solution:

Let the length of the diagonal be x km
Then,

\begin{aligned} \Rightarrow \frac{1}{2} x^{2} = 50 \\ \Rightarrow x^{2} = 100 \\ \Rightarrow x = 10 km \\ \Rightarrow x = (\frac{10}{1.6}) miles \\ \Rightarrow x = 6.25 miles \\ [∵ 1 mile = 1.609 km] \end{aligned}

37. A rectangular plank $\sqrt{2}$ metre wide is placed symmetrically on the diagonal of a square of side 8 metres as shown in the figure. The area of the plank is :

A. $7 \sqrt{2}$ sq. m

B. 14 sq. m

C. 98 sq. m

D. ( $16 \sqrt{2}$ - 3) sq. m

Discuss

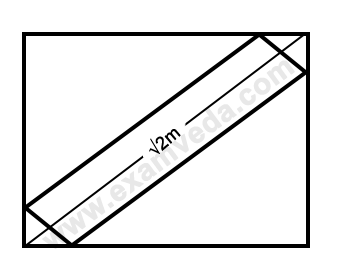
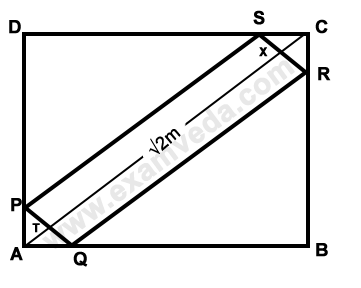
Solution:

\begin{aligned} Let A P = A Q = x metres \\ Then, \\ \Rightarrow x^{2} + x^{2} = {(\sqrt{2})}^{2} \\ \Rightarrow 2 x^{2} = 2 \\ \Rightarrow x^{2} = 1 \\ \Rightarrow x = 1 m \\ S o, △ P A Q is isosceles . \\ ∴ P T = Q T = (\frac{\sqrt{2}}{2}) m = (\frac{1}{\sqrt{2}}) m \\ In △ P T A, we have : ∠ P T A = 90^{\circ} \\ ∴ A T^{2} = A P^{2} - P T^{2} \\ = 1^{2} - {(\frac{1}{\sqrt{2}})}^{2} \\ = 1 - \frac{1}{2} = \frac{1}{2} \\ O r, A T = (\frac{1}{\sqrt{2}}) m \\ Similarly, \\ C X = (\frac{1}{\sqrt{2}}) m \\ ∴ P S = Q R = X T \\ = A C - 2 \times A T \\ = [8 \sqrt{2} - (2 \times \frac{1}{\sqrt{2}})] m \\ = (8 \sqrt{2} - \frac{2}{\sqrt{2}}) m \\ = \frac{14}{\sqrt{2}} m \\ Area of the plank : \\ = (\frac{14}{\sqrt{2}} \times \sqrt{2}) m^{2} \\ = 14 m^{2} \end{aligned}

38. The area of a triangle whose sides are of lengths 3 cm, 4 cm and 5 cm is :

A. 8 cm²

B. 6 cm²

C. 10 cm²

D. None of these

Discuss

Solution:

Since 3² + 4² = 5²,
So it is a right-angled triangle with Base = 3 cm and Height = 4 cm
∴ Area :

\begin{aligned} = (\frac{1}{2} \times 3 \times 4) c m^{2} \\ = 6 c m^{2} \end{aligned}

39. The perimeter of a triangle is 30 cm and its area is 30 cm². If the largest side measures 13 cm, then what is the length of the smallest side of the triangle ?

A. 3 cm

B. 4 cm

C. 5 cm

D. 6 cm

Discuss

Solution:

Let the smallest side be x cm.
Then, other sides are 13 cm and (17 - x) cm
Let a = 13, b = x and c = (17 - x)
So, s = 15

\begin{aligned} Area = \sqrt{s (s - a) (s - b) (s - c)} \\ = \sqrt{15 \times 2 \times (15 - x) (x - 2)} \\ = \sqrt{30 (15 - x) (x - 2)} \\ ∴ 30 (15 - x) (x - 2) = {(30)}^{2} \\ \Rightarrow (15 - x) (x - 2) = 30 \\ \Rightarrow x^{2} - 17 x + 60 = 0 \\ \Rightarrow (x - 12) (x - 5) = 0 \\ \Rightarrow x = 12 or x = 5 \\ Smallest side  =  5 cm \end{aligned}

40. If a parallelogram with area P, a rectangle with area R and a triangle with area T are all constructed on the same base and all have the same altitude, then which of the following statements is false ?

A. P = R

B. P + T = 2R

C. P = 2T

D. T = $\frac{1}{2}$ R

Discuss

Solution:

Let each have base = b and height = h
Then,
P = b × h, R = b × h, T =

\frac{1}{2}

× b × h
So, P = R, P = 2T and T =

\frac{1}{2}

R, are all correct statements.
∴ Option B is false

1 2 3 4 5 6 7 8 9 10

Sign up for our newsletter

Are you passionate about opportunities in the realm of Computer Science within the government sector? Don't miss out on crucial updates, job openings, and career prospects tailored specifically straight to your inbox.

Email address

By subscribing, you agree with our Terms of Service and Privacy Policy.

Resources

Practice PYQ Mock Test

Company

About us Contact us Privacy policy Terms of service

Hashtable