Practice | Hashtable

content Computer Science Arithmetic Aptitude Data Interpretation Logical Reasoning Verbal Reasoning Non-Verbal Reasoning

About About Privacy Policy

Hashtable

Home
Practice
PYQ
Mock Test
Register Free

Home Practice PYQ Mock Test Register Free

Home > Practice > Arithmetic Aptitude > Area > Miscellaneous

21. Twenty-nine times the area of a square is one square metre less than six times the area of the second square and nine times its side exceeds the perimeter of other square by 1 metre. The difference in the sides of these squares is :

A. 5 m

B. $\frac{54}{11}$ m

C. 6 m

D. 11 m

Discuss

Solution:

Let the sides of the two squares be x metres and y metres respectively
Then,

\Rightarrow 29 x^{2} = 6 y^{2} - 1..... (i)

And,

\begin{aligned} \Rightarrow 9 x - 4 y = 1 \\ \Rightarrow 4 y = 9 x - 1 \\ \Rightarrow y = \frac{9 x - 1}{4} . . . . . (i i) \end{aligned}

From (i) and (ii), we get :

\begin{aligned} \Rightarrow 29 x^{2} = 6 {(\frac{9 x - 1}{4})}^{2} - 1 \\ \Rightarrow 29 x^{2} = 6 (\frac{81 x^{2} + 1 - 18 x}{16}) - 1 \\ \Rightarrow 243 x^{2} + 3 - 54 x - 8 = 232 x^{2} \\ \Rightarrow 11 x^{2} - 54 x - 5 = 0 \\ \Rightarrow (x - 5) (11 x + 1) = 0 \\ \Rightarrow x = 5 m \\ ∴ y = \frac{9 x - 1}{4} = \frac{9 \times 5 m - 1}{4} = 11 m \\ Required difference \\ = (11 - 5) m \\ = 6 m \end{aligned}

22. In ΔPQR, side PQ = 3 cm and side PR = 25 cm. What is the area of ΔPQR ?

A. $2 \sqrt{154} sq .cm$

B. $3 \sqrt{154} sq .cm$

C. $4 \sqrt{308} sq .cm$

D. Cannot be determined

Discuss

Solution:

\begin{aligned} Area of Δ P Q R \\ = \frac{1}{2} \times Q R \times P Q \\ Given, P Q = 3 c m \\ Q R = \sqrt{{(P R)}^{2} - {(P Q)}^{2}} \\ = \sqrt{{(25)}^{2} - 3^{2}} c m \\ = \sqrt{625 - 9} c m \\ = \sqrt{616} c m \\ = 2 \sqrt{154} c m \\ ∴ Area of Δ P Q R \\ = (\frac{1}{2} \times 2 \sqrt{154} \times 3) c m^{2} \\ = 3 \sqrt{154} c m^{2} \end{aligned}

23. In an isosceles triangle, the measure of each of the equal sides is 10 cm and the angle between them is 45° . The area of the triangle is :

A. $25 c m^{2}$

B. $\frac{25}{2} \sqrt{2} c m^{2}$

C. $25 \sqrt{2} c m^{2}$

D. $25 \sqrt{3} c m^{2}$

Discuss

Solution:

\begin{aligned} Area of the traingle : \\ = \frac{1}{2} a b \sin θ \\ = (\frac{1}{2} \times 10 \times 10 \times \sin 45^{\circ}) c m^{2} \\ = (\frac{1}{2} \times 10 \times 10 \times \frac{1}{\sqrt{2}}) c m^{2} \\ = (\frac{50}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}) c m^{2} \\ = 25 \sqrt{2} c m^{2} \end{aligned}

24. A triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is 100 m, then the altitude of the triangle is :

A. 10 $\sqrt{2}$ m

B. 100 m

C. 100 $\sqrt{2}$ m

D. 200 m

Discuss

Solution:

Let the altitude of the triangle be h₁ and base of each be b.
Then,

\frac{1}{2}

× b₁ × h₁ = b × h₂, where h₂ = 100 m
⇔ h₁ = 2 h₂
⇔ h₁ = (2 × 100) m
⇔ h₁ = 200 m

25. The circumference of a circle, whose area is 24.64 m² , is :

A. 14.64 m

B. 16.36 m

C. 17.60 m

D. 18.40 m

Discuss

Solution:

\begin{aligned} ∵ π R^{2} = 24.64 \\ \Leftrightarrow R^{2} = (\frac{24.64}{22} \times 7) \\ \Leftrightarrow R^{2} = 7.84 \\ \Leftrightarrow R = \sqrt{7.84} \\ \Leftrightarrow R = 2.8 m \\ ∴ Circumference : \\ = (2 \times \frac{22}{7} \times 2.8) m \\ = 17.60 m \end{aligned}

26. The ratio of the radii of two circle is 3 : 2. What is the ratio of their circumferences ?

A. 2 : 3

B. 3 : 2

C. 4 : 9

D. None of these

Discuss

Solution:

Let the radii of the two circle be 3r and 2r respectively
Then, required ratio :

\begin{aligned} = \frac{2 π (3 r)}{2 π (2 r)} \\ = \frac{3}{2} \\ = 3 : 2 \end{aligned}

27. A circular grassy plot of land, 42 cm is diameter, has a path 3.5 m wide running around it outside. The cost of gravelling the path at Rs. 4 per square metre is :

A. Rs. 1002

B. Rs. 1802

C. Rs. 2002

D. Rs. 3002

Discuss

Solution:

Radius of the plot = 21 m
Area of the path :

\begin{aligned} = π [{(24.5)}^{2} - {(21)}^{2}] m^{2} \\ = [π (24.5 + 21) (24.5 - 21)] m^{2} \\ = (\frac{22}{7} \times 45.5 \times 3.5) m^{2} \\ = 500.5 m^{2} \end{aligned}

∴ Cost of gravelling :
= Rs. (500.5 × 4)
= Rs. 2002

28. A horse is tied at the corner of a rectangular field whose length is 20 m and width is 16 m, with a rope whose length is 14 m. Find the area which the horse can graze :

A. 144 sq. m

B. 154 sq. m

C. 156 sq. m

D. 164 sq. m

Discuss

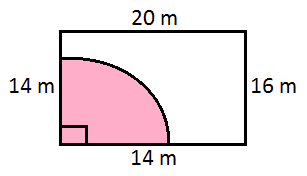
Solution:

Required area = Area of the quadrant with radius 14 m :

\begin{aligned} = (\frac{22}{7} \times 14 \times 14 \times \frac{90}{360}) m^{2} \\ = 154 m^{2} \end{aligned}

29. A triangle with sides 13 cm, 14 cm and 15 cm is inscribed in a circle. The radius of the circle is :

A. 2 cm

B. 3 cm

C. 4 cm

D. 8.125 cm

Discuss

Solution:

\begin{aligned} s = \frac{13 + 14 + 15}{2} = \frac{42}{2} = 21 \\ ∴ △ = \sqrt{21 \times 8 \times 7 \times 6} \\ = \sqrt{s (s - a) (s - b) (s - c)} \\ = (2 \times 2 \times 3 \times 7) \\ = 84 c m^{2} \end{aligned}

Radius of circle :

\begin{aligned} = (\frac{13 \times 14 \times 15}{4 \times 84}) c m^{2} \\ = (\frac{65}{8}) c m \\ = 8.125 c m \end{aligned}

30. A skating champion moves along the circumference of a circle of radius 28 m in 44 sec. How many seconds will it take her to move along the perimeter of a hexagon of side 48 m ?

A. 48 sec

B. 68 sec

C. 72 sec

D. 84 sec

Discuss

Solution:

Distance mode by the skater in 44 sec
= Circumference of the circle
=

(2 \times \frac{22}{7} \times 28)

m
= 176 m
Speed of skater :
=

(\frac{176}{44})

m/sec
= 4 m/sec
Perimeter of hexagon :
= (6 × 48) m
= 288 m
∴ Required difference :
=

(\frac{288}{4})

sec
= 72 sec

1 2 3 4 5 6 7 8 9 10

Sign up for our newsletter

Are you passionate about opportunities in the realm of Computer Science within the government sector? Don't miss out on crucial updates, job openings, and career prospects tailored specifically straight to your inbox.

Email address

By subscribing, you agree with our Terms of Service and Privacy Policy.

Resources

Practice PYQ Mock Test

Company

About us Contact us Privacy policy Terms of service

Hashtable